Table of Links
2. Mathematical Description and 2.1. Numerical Algorithms for Nonlinear Equations
2.4. Matrix Coloring & Sparse Automatic Differentiation
3.1. Composable Building Blocks
3.2. Smart PolyAlgortihm Defaults
3.3. Non-Allocating Static Algorithms inside GPU Kernels
3.4. Automatic Sparsity Exploitation
3.5. Generalized Jacobian-Free Nonlinear Solvers using Krylov Methods
4. Results and 4.1. Robustness on 23 Test Problems
4.2. Initializing the Doyle-Fuller-Newman (DFN) Battery Model
4.3. Large Ill-Conditioned Nonlinear Brusselator System

where
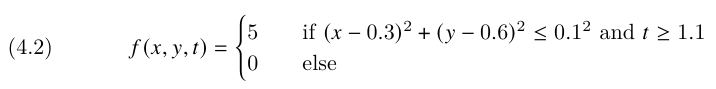
and the initial conditions are
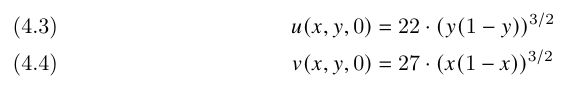
with the periodic boundary condition
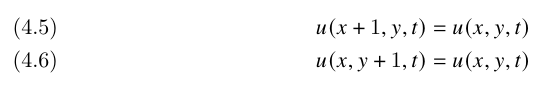
We analyze our solvers for this problem in 3 parts. Firstly, Figure 10 compares the scaling of NewtonRaphson and TrustRegion between frameworks. NonlinearSolve.jl leverages sparsity detection and colored sparse matrix algorithms to accelerate Jacobian construction and is consistently faster than all existing solvers here. None of the frameworks have built-in sparsity support and, unsurprisingly, don’t scale well. However, with increasing discretization, explicitly forming Jacobians eventually becomes infeasible. Figure 11 demonstrates NonlinearSolve.jl Jacobian-free Krylov Methods with Preconditioning that solve the linear system without constructing the Jacobian. We note that Sundials KINSOL with their built-in GMRES fails to converge to the solution, and MINPACK and NLsolve.jl don’t support Jacobian-Free methods.
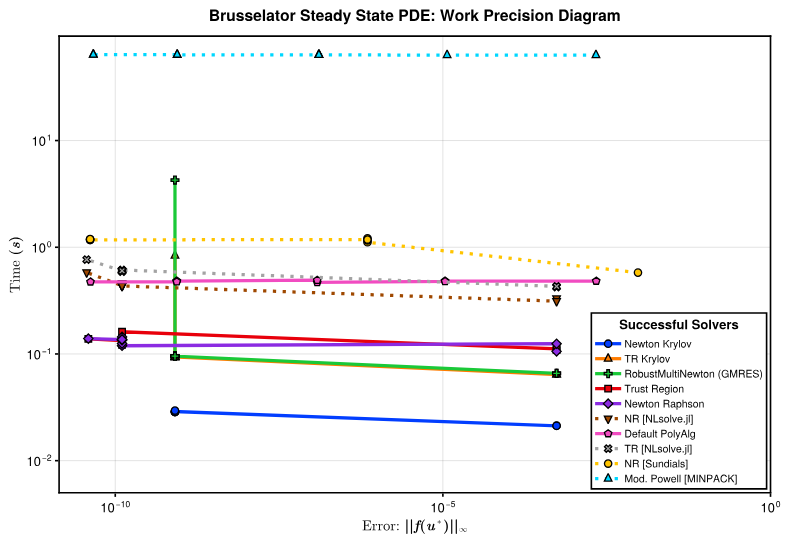
Finally, in Figure 12, we present a Work-Precision Diagram for the discretized Brusselator on a 32 × 32 grid, showing that our methods are an order of magnitude faster than the ones in other software.
:::info
This paper is available on arxiv under CC BY 4.0 DEED license.
:::
:::info
Authors:
(1) AVIK PAL, CSAIL MIT, Cambridge, MA;
(2) FLEMMING HOLTORF;
(3) AXEL LARSSON;
(4) TORKEL LOMAN;
(5) UTKARSH;
(6) FRANK SCHÄFER;
(7) QINGYU QU;
(8) ALAN EDELMAN;
(9) CHRIS RACKAUCKAS, CSAIL MIT, Cambridge, MA.
:::