Reinforcement Learning Simulation Metrics: QQ plots, ACF graphs, and Volatility Analysis

:::tip
This is Part 10 of a 11-part series based on the research paper “Reinforcement Learning In Agent-based Market Simulation: Unveiling Realistic Stylized Facts And Behavior”. Use the table of links below to navigate to the next part.

:::

Table of Links

Part 1: Abstract & Introduction

Part 2: Important Concepts

Part 3: System Description

Part 4: Agents & Simulation Details

Part 5: Experiment Design

Part 6: Continual Learning

Part 7: Experiment Results

Part 8: Market and Agent Responsiveness to External Events

Part 9: Conclusion & References

Part 10: Additional Simulation Results

Part 11: Simulation Configuration

7 Appendix

7.1 Additional Simulation Results

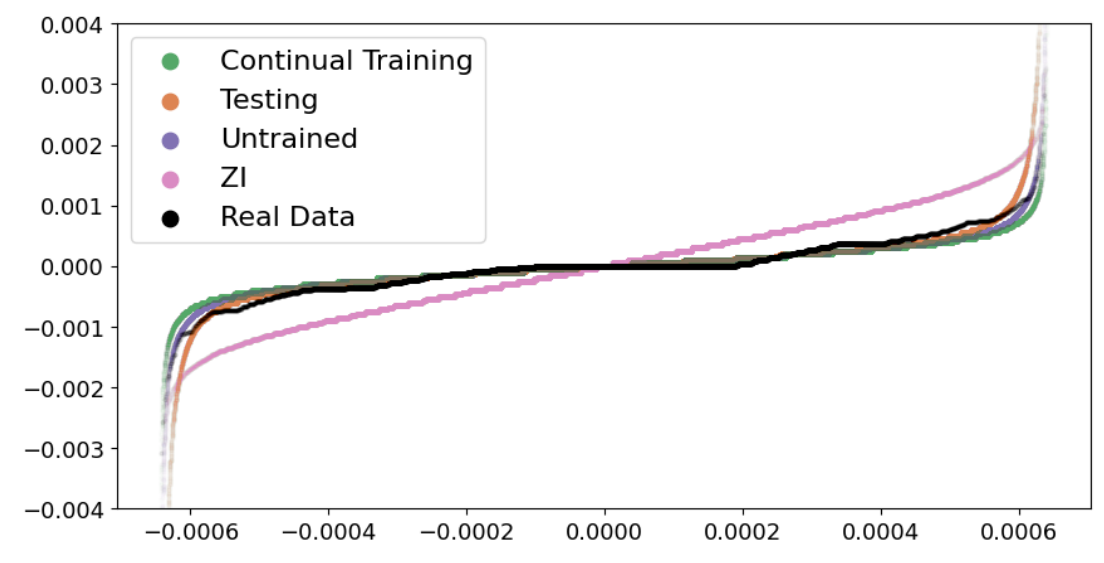
Figure 1 is the QQ plot for simulations’ prices(10 seconds) generated with all five groups of setup, providing additional insights to Figure 3a. More details in section 5.1.

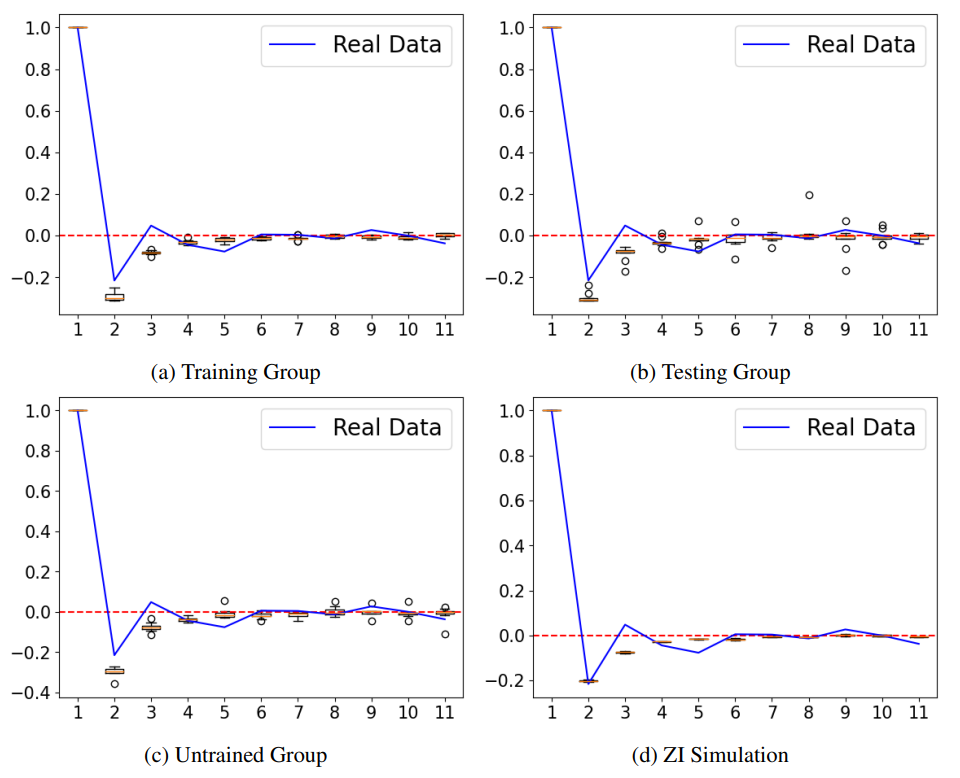
Figure 2 shows the ACF graphs for the price returns from groups of testing and untrained. More details in section 5.1.

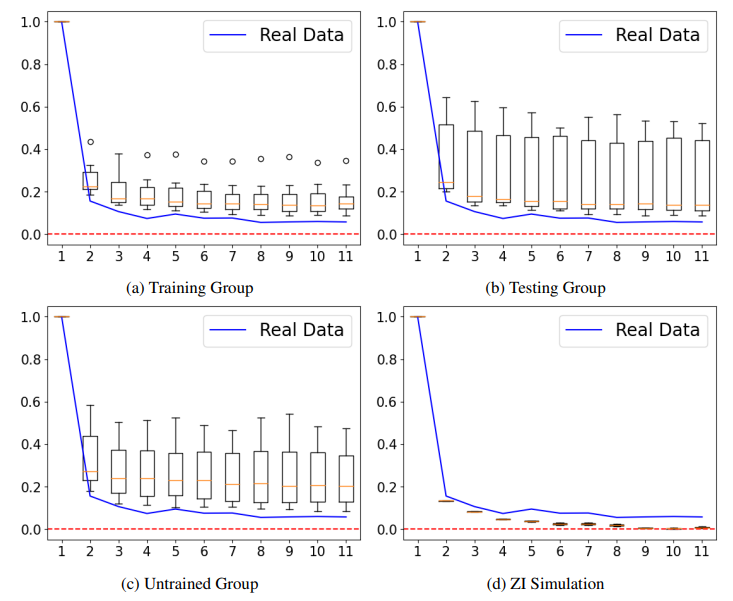
Figure 3 shows the ACF graphs for the absolute price returns from groups of testing and untrained. More details in section 5.1.

Figure 4 shows the volatility clustering analysis graphs for groups of testing and untrained. The analysis method can be found in [1]. More details in section 5.1.

Table 1 provides additional market characteristics (Kurtosis and Inventory Risk) for groups of continual train, testing, and non train.

:::info
Authors:

(1) Zhiyuan Yao, Stevens Institute of Technology, Hoboken, New Jersey, USA (zyao9@stevens.edu);

(2) Zheng Li, Stevens Institute of Technology, Hoboken, New Jersey, USA (zli149@stevens.edu);

(3) Matthew Thomas, Stevens Institute of Technology, Hoboken, New Jersey, USA (mthomas3@stevens.edu);

(4) Ionut Florescu, Stevens Institute of Technology, Hoboken, New Jersey, USA (ifloresc@stevens.edu).

:::

---

:::info
This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.

:::