Mathematical Proofs for Fair AI Bias Analysis

Table of Links

Abstract and 1 Introduction

2 Related Works

3 Preliminaries

3.1 Fair Supervised Learning and 3.2 Fairness Criteria

3.3 Dependence Measures for Fair Supervised Learning

4 Inductive Biases of DP-based Fair Supervised Learning

4.1 Extending the Theoretical Results to Randomized Prediction Rule

5 A Distributionally Robust Optimization Approach to DP-based Fair Learning

6 Numerical Results

6.1 Experimental Setup

6.2 Inductive Biases of Models trained in DP-based Fair Learning

6.3 DP-based Fair Classification in Heterogeneous Federated Learning

7 Conclusion and References

Appendix A Proofs

Appendix B Additional Results for Image Dataset

Appendix A Proofs

A.1 Proof of Theorem 1

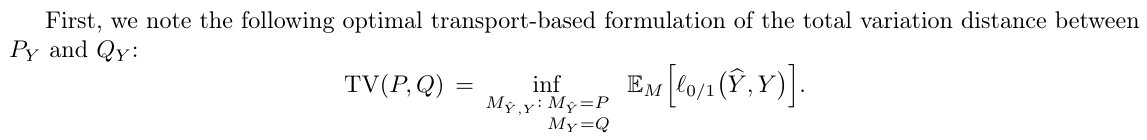
Therefore, for the objective function in Equation (1), we can write the following:

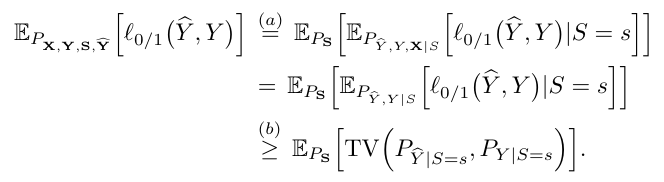
Knowing that TV is a metric distance satisfying the triangle inequality, the above equations show that

Therefore,

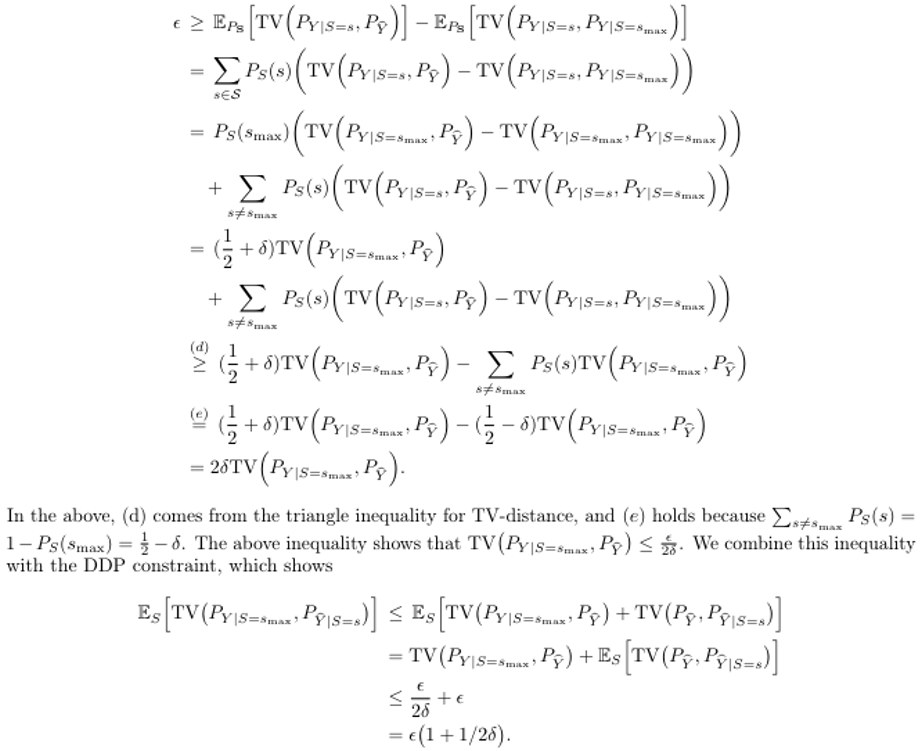
A.2 Proof of Theorem 2

A.3 Proof of Theorem 3

Therefore, we can follow the proof of Theorems 1,2 which shows the above inequality leads to the bounds claimed in the theorems.

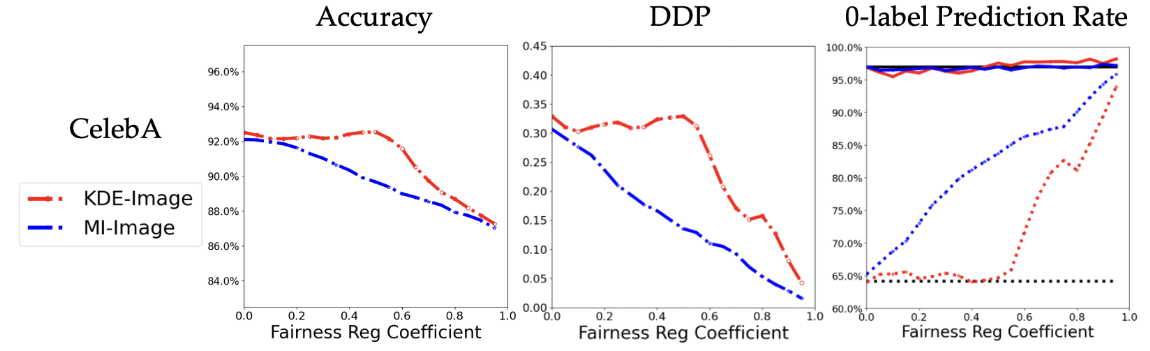
Appendix B Additional Results for Image Dataset

This part shows the inductive biases of DP-based fair classifier for CelebA dataset, as well as the visualized plots. For the baselines, two fair classifiers are implemented for image fair classification: KDE proposed by [11] and MI proposed by [6], based on ResNet-18 [28].

:::info
This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.

:::

---

:::info
Authors:

(1) Haoyu LEI, Department of Computer Science and Engineering, The Chinese University of Hong Kong (hylei22@cse.cuhk.edu.hk);

(2) Amin Gohari, Department of Information Engineering, The Chinese University of Hong Kong (agohari@ie.cuhk.edu.hk);

(3) Farzan Farnia, Department of Computer Science and Engineering, The Chinese University of Hong Kong (farnia@cse.cuhk.edu.hk).

:::