Table of Links
2. Mathematical Description and 2.1. Numerical Algorithms for Nonlinear Equations
2.4. Matrix Coloring & Sparse Automatic Differentiation
3.1. Composable Building Blocks
3.2. Smart PolyAlgortihm Defaults
3.3. Non-Allocating Static Algorithms inside GPU Kernels
3.4. Automatic Sparsity Exploitation
3.5. Generalized Jacobian-Free Nonlinear Solvers using Krylov Methods
4. Results and 4.1. Robustness on 23 Test Problems
4.2. Initializing the Doyle-Fuller-Newman (DFN) Battery Model
4.3. Large Ill-Conditioned Nonlinear Brusselator System
2. Mathematical Description
This section introduces the mathematical framework for numerically solving nonlinear problems and demonstrates the built-in support for such problems in NonlinearSolve.jl. A nonlinear problem is defined as:

where J𝑘 is the Jacobian of 𝑓 (𝑢, 𝜃) with respect to 𝑢, evaluated at 𝑢𝑘. This method exhibits rapid convergence [23, Theorem 11.2] when the initial guess is sufficiently close to a root. Furthermore, it requires only the function and its Jacobian, making it computationally efficient for many practical applications. Halley’s method enhances the Newton-Raphson method, leveraging information from the second total derivative of the function to achieve cubic convergence. It refines the initial guess 𝑢0 using:
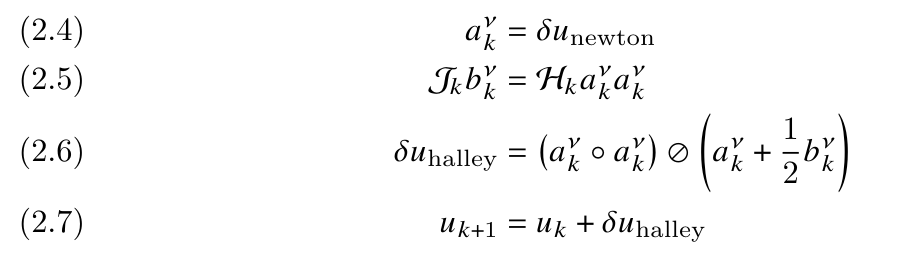
![Fig. 1: NonlinearSolve.jl allows seamless switching between different line search routines. Instead of nothing, we can specify HagerZhang(), BackTracking(), MoreTheunte(), StrongWolfe(), or LiFukushimaLineSearch() to opt-in to using line search. Line search enables NewtonRaphson to converge faster on the Generalized Rosenbrock Problem [Equation (2.12)], while it fails to converge without a line search.](https://cdn.hackernoon.com/images/fWZa4tUiBGemnqQfBGgCPf9594N2-afa3w1u.png)

This method provides higher convergence orders without reliance on higher-order derivatives. [25] summarizes other multi-step schemes that provide higher-order convergence using only first-order derivatives. These methods are local algorithms, and their convergence relies on having a good initial guess. We will discuss some techniques to facilitate the global convergence of these methods in the following section.
:::info
This paper is available on arxiv under CC BY 4.0 DEED license.
:::
[5] For Halley’s method, we additionally assume twice-differentiability.
:::info
Authors:
(1) AVIK PAL, CSAIL MIT, Cambridge, MA;
(2) FLEMMING HOLTORF;
(3) AXEL LARSSON;
(4) TORKEL LOMAN;
(5) UTKARSH;
(6) FRANK SCHÄFER;
(7) QINGYU QU;
(8) ALAN EDELMAN;
(9) CHRIS RACKAUCKAS, CSAIL MIT, Cambridge, MA.
:::