Making Sense of AI Learning Proofs

:::info
Authors:

(1) Jongmin Lee, Department of Mathematical Science, Seoul National University;

(2) Ernest K. Ryu, Department of Mathematical Science, Seoul National University and Interdisciplinary Program in Artificial Intelligence, Seoul National University.

:::

Abstract and 1 Introduction

1.1 Notations and preliminaries

1.2 Prior works

2 Anchored Value Iteration

2.1 Accelerated rate for Bellman consistency operator

2.2 Accelerated rate for Bellman optimality opera

3 Convergence when y=1

4 Complexity lower bound

5 Approximate Anchored Value Iteration

6 Gauss–Seidel Anchored Value Iteration

7 Conclusion, Acknowledgments and Disclosure of Funding and References

A Preliminaries

B Omitted proofs in Section 2

C Omitted proofs in Section 3

D Omitted proofs in Section 4

E Omitted proofs in Section 5

F Omitted proofs in Section 6

G Broader Impacts

H Limitations

F Omitted proofs in Section 6

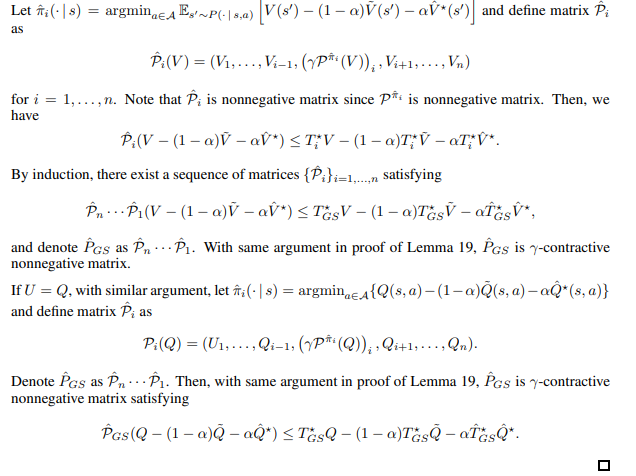
Next, we prove following key lemma

Proof of Lemma 21. First, we prove first inequality in Lemma 21 by induction.

If k= 0,

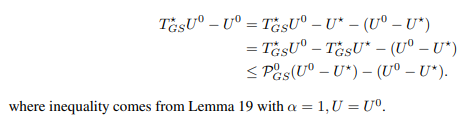
By induction,

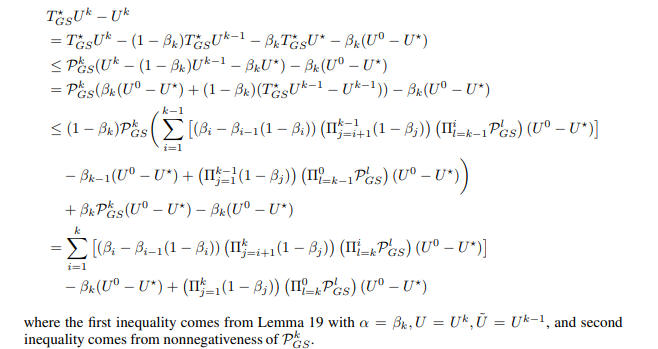
First, we prove second inequality in Lemma 21 by induction.

If k= 0,

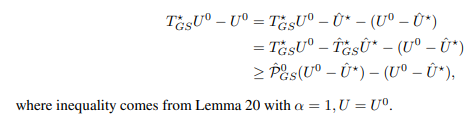
By induction.

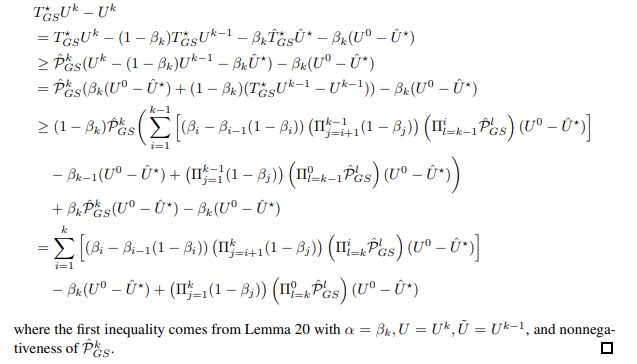
Now, we prove the first rate in Theorem 7.

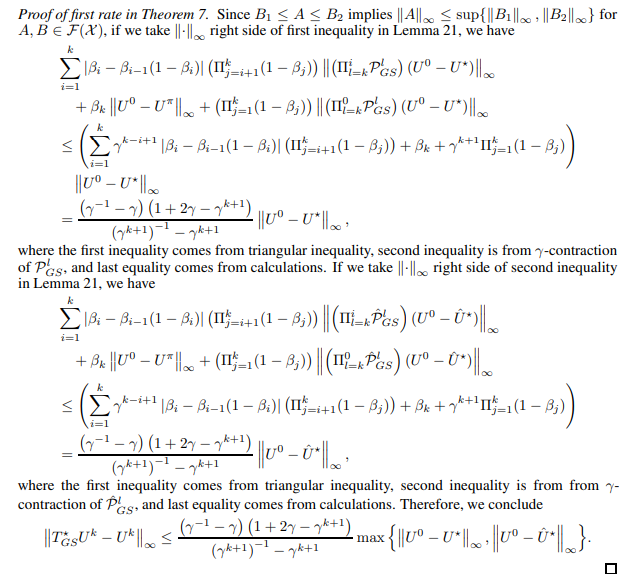
For the second rates of Theorem 7, we introduce following lemma.

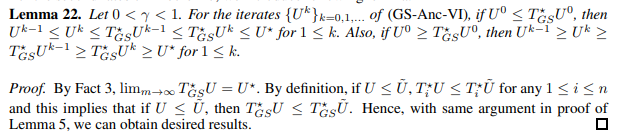
Now, we prove the second rates in Theorem 7.

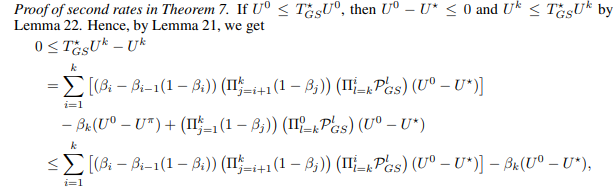
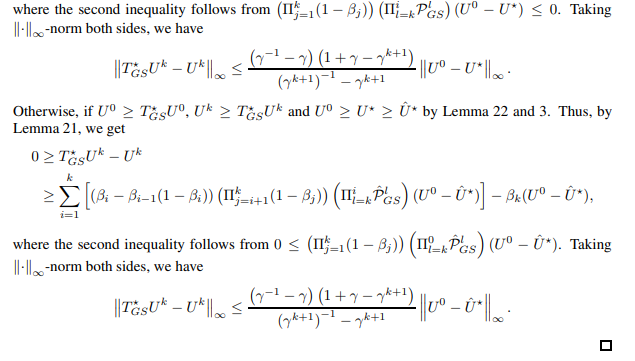
:::info
This paper is available on arxiv under CC BY 4.0 DEED license.

:::