Graph Embeddings and Node Learning on Grassmann Manifolds

Table of Links

Abstract and 1. Introduction

2. Preliminaries

3. Proposed Approach

   3.1 Notation

   3.2 Nueral Networks on SPD Manifolds

   3.3 MLR in Structure Spaces

   3.4 Neural Networks on Grassmann Manifolds

4. Experiments

5. Conclusion and References

A. Notations

B. MLR in Structure Spaces

C. Formulation of MLR from the Perspective of Distances to Hyperplanes

D. Human Action Recognition

E. Node Classification

F. Limitations of our work

G. Some Related Definitions

H. Computation of Canonical Representation

I. Proof of Proposition 3.2

J. Proof of Proposition 3.4

K. Proof of Proposition 3.5

L. Proof of Proposition 3.6

M. Proof of Proposition 3.11

N. Proof of Proposition 3.12

3.4 NEURAL NETWORKS ON GRASSMANN MANIFOLDS

In this section, we present a method for computing the Grassmann logarithmic map in the projector perspective. We then propose GCNs on Grassmann manifolds.

3.4.1 GRASSMANN LOGARITHMIC MAP IN THE PROJECTOR PERSPECTIVE

The Grassmann logarithmic map is given (Batzies et al., 2015; Bendokat et al., 2020) by

Proof See Appendix N.

3.4.2 GRAPH CONVOLUTIONAL NETWORKS ON GRASSMANN MANIFOLDS

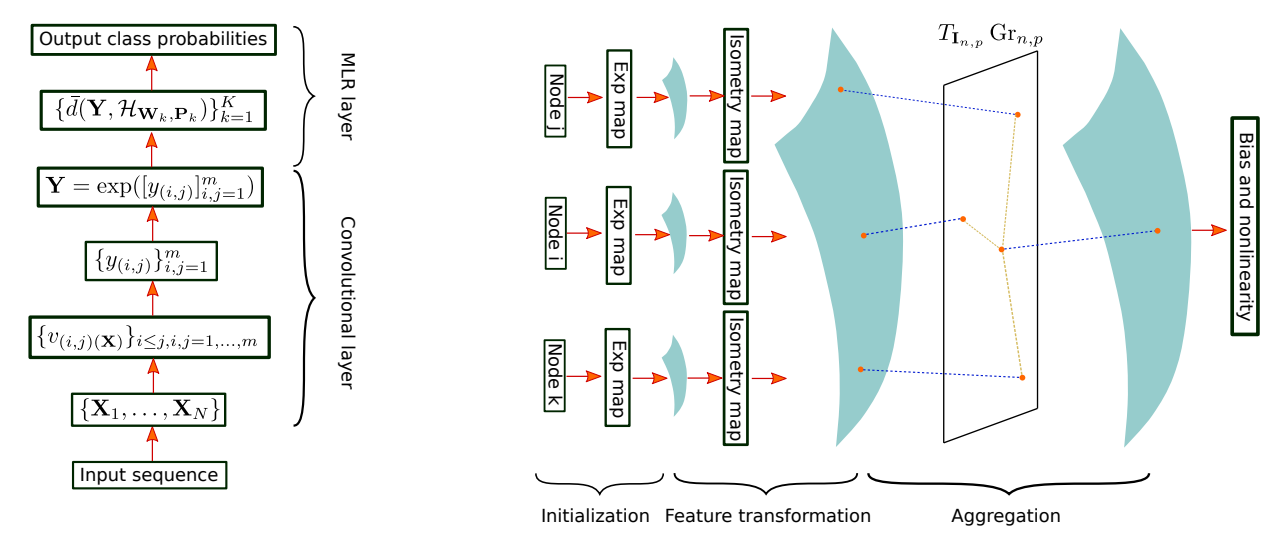
The Grassmann logarithmic maps in the aggregation operation are obtained using Proposition 3.12.

Another approach for embedding graphs on Grassmann manifolds has also been proposed in Zhou et al. (2022). However, unlike our method, this method creates a Grassmann representation for a graph via a SVD of the matrix formed from node embeddings previously learned by a Euclidean neural network. Therefore, it is not designed to learn node embeddings on Grassmann manifolds.

:::info
Authors:

(1) Xuan Son Nguyen, ETIS, UMR 8051, CY Cergy Paris University, ENSEA, CNRS, France (xuan-son.nguyen@ensea.fr);

(2) Shuo Yang, ETIS, UMR 8051, CY Cergy Paris University, ENSEA, CNRS, France (son.nguyen@ensea.fr);

(3) Aymeric Histace, ETIS, UMR 8051, CY Cergy Paris University, ENSEA, CNRS, France (aymeric.histace@ensea.fr).

:::

---

:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.

:::