Why Sparse Spectral Training Might Replace LoRA in AI Model Optimization

Table of Links

Abstract and 1. Introduction

2. Related Work

3. Low Rank Adaptation

   3.1 LoRA and 3.2 Limitation of LoRA

   3.3 ReLoRA*

4. Sparse Spectral Training

   4.1 Preliminaries and 4.2 Gradient Update of U, VT with Σ

   4.3 Why SVD Initialization is Important

   4.4 SST Balances Exploitation and Exploration

   4.5 Memory-Efficient Implementation for SST and 4.6 Sparsity of SST

5. Experiments

   5.1 Machine Translation

   5.2 Natural Language Generation

   5.3 Hyperbolic Graph Neural Networks

6. Conclusion and Discussion

7. Broader Impacts and References

Supplementary Information

A. Algorithm of Sparse Spectral Training

B. Proof of Gradient of Sparse Spectral Layer

C. Proof of Decomposition of Gradient of Weight

D. Proof of Advantage of Enhanced Gradient over Default Gradient

E. Proof of Zero Distortion with SVD Initialization

F. Experiment Details

G. Singular Value Pruning

H. Evaluating SST and GaLore: Complementary Approaches to Memory Efficiency

I. Ablation Study

4 Sparse Spectral Training

To address the limitations discussed previously, this section introduces Sparse Spectral Training (SST) and its detailed implementation.

4.1 Preliminaries

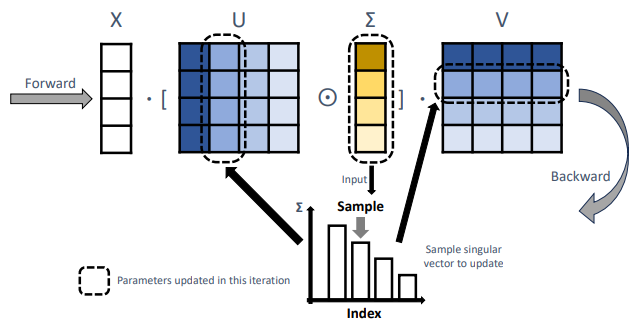
Sparse Spectral Training (SST) leverages sparse updates within the spectral domain of neural network weights. By updating singular vectors selectively based on their associated singular values, SST prioritizes the most significant spectral components. This transforms each linear layer as follows:

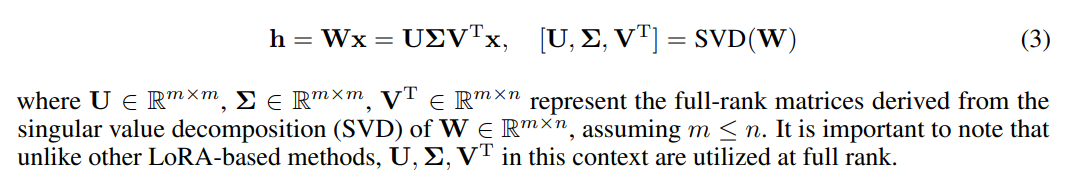
4.2 Gradient Update of U, VT with Σ

Update Σ. The diagonal matrix Σ, simplified as a vector of dimension m, is updated every step due to its low memory overhead. This ensures that all singular values are consistently adjusted to refine the model’s performance. The update is as follows:

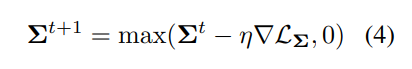
where η represents the learning rate, and ∇LΣ is the gradient backpropagated to Σ. The max function with zero ensures that Σ values remain nonnegative.

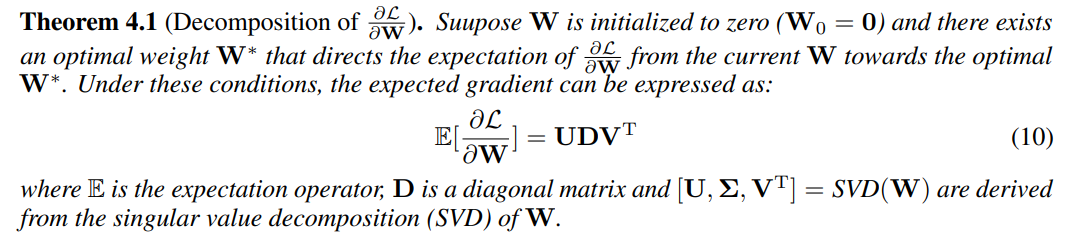
This theorem indicates that the enhanced gradient more closely approximates full-rank updates per iteration compared to the standard approach. Specifically, the default gradient’s dependence on Σi for magnitude could result in smaller updates if the current Σi is low, potentially stalling training. By decoupling the update mechanisms for direction and magnitude, the enhanced gradient method mitigates this issue.

Theorem 4.2 indicates that the enhanced gradient more closely approximates full-rank training in each step update, than the default gradient (proof in Appendix D). Specifically, the default gradient’s dependence on Σi could result in smaller updates if the current Σi is low, potentially stalling training. By decoupling the update mechanisms for direction (U·i and V·i) and magnitude (Σi), the enhanced gradient method mitigates this issue:

Each time we perform this Re-SVD, we consider it a new round. Each time we select vectors for updating, as described in Eq. 5, we call it a new iteration. The full method is detailed in Algorithm 2.

4.3 Why SVD Initialization is Important

This section outlines the advantages of using SVD initialization and periodic Re-SVD over zero initialization as employed in LoRA and ReLoRA methods.

Saddle Point Issues with Zero Initialization. Using zero initialization, the gradient updates for matrices A and B can lead to stagnation at saddle points. The gradient of A and B in Eq. 1 is:

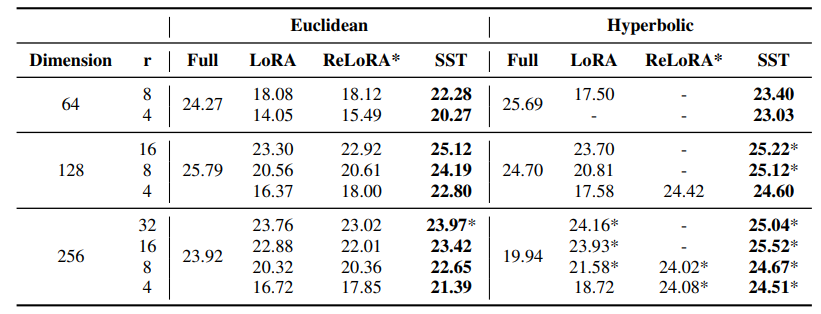
4.4 SST Balances Exploitation and Exploration

From another prospective, SST combines the strategies of exploitation and exploration in spectral domain. In contrast, LoRA primarily focuses on exploitation by repeatedly adjusting the top-r singular values, as detailed in Section 3.2, neglecting the remaining spectral vectors. ReLoRA*, on the other hand, emphasizes exploration by periodically reinitializing the matrices B and A after each merging, thereby constantly seeking new directions for learning but ignoring previously established dominant directions.

4.5 Memory-Efficient Implementation for SST

4.6 Sparsity of SST

:::info
Authors:

(1) Jialin Zhao, Center for Complex Network Intelligence (CCNI), Tsinghua Laboratory of Brain and Intelligence (THBI) and Department of Computer Science;

(2) Yingtao Zhang, Center for Complex Network Intelligence (CCNI), Tsinghua Laboratory of Brain and Intelligence (THBI) and Department of Computer Science;

(3) Xinghang Li, Department of Computer Science;

(4) Huaping Liu, Department of Computer Science;

(5) Carlo Vittorio Cannistraci, Center for Complex Network Intelligence (CCNI), Tsinghua Laboratory of Brain and Intelligence (THBI), Department of Computer Science, and Department of Biomedical Engineering Tsinghua University, Beijing, China.

:::

---

:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.

:::