:::info
Authors:
:::
Table Of Links
2 FLATTENING AND ARC APPROXIMATION OF CURVES
3 EULER SPIRALS AND THEIR PARALLEL CURVES
5 ERROR METRICS FOR APPROXIMATION BY ARCS
7 CONVERSION FROM CUBIC BÉZIERS TO EULER SPIRALS
CONCLUSIONS, FUTURE WORK AND REFERENCES
ABSTRACT
Vector graphics includes both filled and stroked paths as the main primitives. While there are many techniques for rendering filled paths on GPU, stroked paths have proved more elusive. This paper presents a technique for performing stroke expansion, namely the generation of the outline representing the stroke of the given input path. Stroke expansion is a global problem, with challenging constraints on continuity and correctness.
Nonetheless, we implement it using a fully parallel algorithm suitable for execution in a GPU compute shader, with minimal preprocessing. The output of our method can be either line or circular arc segments, both of which are well suited to GPU rendering, and the number of segments is minimal. We introduce several novel techniques, including an encoding of vector graphics primitives suitable for parallel processing, and an Euler spiral based method for computing approximations to parallel curves and evolutes.
INTRODUCTION
Stroke rendering is an essential part of the standard vector graphics imaging model. The standard representation of paths is a sequence of cubic Bézier segments. While there are a number of published techniques for GPU rendering of filled paths, stroke rendering is more challenging to parallelize, largely because path segments cannot be processed independently of each other; rendering of the joins between path segments depends on both adjoining segments, and the endpoints of paths (when not closed) are rendered with caps.
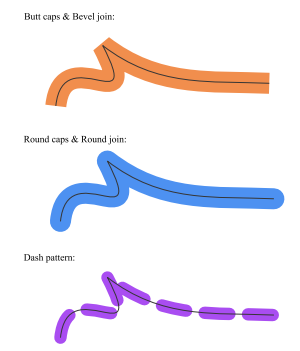
Joins and caps can be rendered with a variety of styles within the same document. The style of stroke rendering also optionally includes dashing, which applies a pattern of dashes and gaps to the outline of the shape, as illustrated in Figure 1. A typical vector graphics document may have thousands of stroked paths. A map or CAD drawing may have tens of thousands of paths, possibly consisting of millions of path segments.
At this scale, the computational cost of stroke rendering on a CPU may result in loss of interactive rendering performance. We believe the runtime performance can be improved significantly by offloading stroke rendering to a GPU. This requires that the algorithm be GPUfriendly: that it exploit the available parallelism, be work efficient, and avoid unnecessarily complex and divergent control flow. It must also remain numerically robust when computed with 32-bit floating pointing numbers.
There are a number of strategies for rendering strokes. Among them are local techniques that break down the stroke into individual closed primitives, distance field techniques (or similar techniques based on point inclusion). In this paper, we focus on stroke expansion, the generation of an outline that, when filled, represents the rendered stroke. Implementing stroke rendering using stroke expansion enables a unified approach to rendering both filled and stroked paths downstream.
Among other benefits, such an approach avoids a large number of draw calls when stroked and filled paths are finely interleaved, as is often the case. Correctness is another challenging aspect of stroke rendering. We propose that the correctness of stroke outlines be divided into weak correctness and strong correctness. We define strong correctness as the computation of the outline of a line swept along the segment, maintaining normal orientation, combined with stroke caps and joins.
Weak correctness, by contrast, only requires the parallel curves (also known as “offset curves”) of path segments, combined with caps and the outer contours of joins. Both Nehab [2020] and Kilgard [2020b] provide useful definitions of strongly correct stroke rendering, and Nehab in particular describes how to achieve it in stroke expansion.
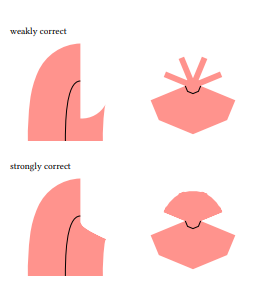
Briefly, when the path curvature exceeds the reciprocal of the stroke half-width, evolute segments are required in addition to the parallel curves, as well asinner contours of joins when segments are short. The technique described in this paper produces strongly correct outlines according to this definition. Examples of weakly and strongly correct rendering are shown in Figure 2. Correct stroke rendering also relies on accurate approximation of the parallel curves of the input paths. Determining the parallel curve of a cubic Bézier is not analytically tractable, as it is a tenth order algebraic formula [4].
Thus, all practical stroke rendering techniques employ an approximation, with error tolerance as a tunable parameter, typically representing the maximum allowable Fréchet distance between the true curve and its approximation. A typical value is 0.25 device pixel, as that is close to the threshold of visibility. A correct algorithm will produce an approximate curve within the error tolerance, but an efficient algorithm will not subdivide significantly more than is necessary to meet the error bound. Some specifications for vector graphics, including PDF [10], specify the error tolerance explicitly.
The subproblem of approximating parallel curves has spawned extensive literature, none of which is entirely satisfying, especially when it comes to algorithms that can be efficiently evaluated on GPU. An example of a reasonably good algorithm that computes flattened parallel curves is Yzerman [2020], as used in the Blend2D rendering library. For producing curved outlines, the Tiller and Hanson [23] algorithm is commonly implemented and cited, but its performance is quite poor when applied to cubic Béziers. The quadratic Bézier version is adequate, and forms the basis of the algorithm in Nehab [2020].
A variant is also used in Skia [8]; instead of lowering the cubic Bézier to a quadratic approximation and then computing the parallel curve, Skia approximates the parallel curve directly with a quadratic Bézier, then measures the error to determine whether further subdivision is necessary.
Previous work on stroke rendering does not fully solve the problem of fast and correct stroking. Most existing implementations have correctness problems, in particular failing to draw the evolutes and inner joins as required for strong correctness; Nehab [2020] provides a detailed survey. In addition, most implementations are not suitable for running on GPU, requiring sequential execution to produce watertight outlines.
One GPU implementation is polar stroking (Kilgard [2020b]), a local technique, but among other limitations, it does not bound the Fréchet distance error (rather, it bounds the angle error). Our central approach bounding the error tolerance is error metrics, which predict the Fréchet distance error. The error metrics presented in this paper are both straightforward to compute, and also invertible, which avoids excessive subdivision and also increases the amount of available parallelism to exploit.
Previous approaches to error measurement generally follow a “cut then measure” approach, where the approximate curve is generated, then the error measured by sampling. Such sampling is often time consuming, involving iteration, and even then risks underestimating the error due to inadequate sampling. Previous work, particularly Kilgard [2020b], has explained how to break the input path into dash segments of the specified length on GPU using a prefix sum of segment arc lengths.
There are implementation tradeoffs to GPU-based dash processing, including potentially a larger number of dispatch stages. We anticipate that the potential performance benefit of implementing dashing on a GPU depends on the scene and other factors in the overall rendering pipeline. While we would expect further performance improvement from GPU-based dashing, we did not fully explore the solution space and we were able to achieve acceptable performance with dash processing on CPU.
This paper presents a solution to the core problem of stroke expansion, well suited to GPU implementation. It can produce both flattened polylines or an approximation consisting of circular arcs. The best choice depends on the capabilities of the path rendering mechanism following stroke expansion, but as we show, outlines consisting of circular arcs have many fewer segments and are correspondingly faster to produce.
The algorithm is based on Euler spiral segments as an intermediate representation, with an iterative algorithm based on a straightforward error metric for conversion from cubic Béziers. We have also devised a compact binary encoding of paths, suitable for fully parallel computation of stroke outlines, while requiring minimal CPU-side processing. Our algorithm has been implemented in GPU compute shaders, integrated in a full rendering engine for vector graphics, and shows a dramatic speedup over CPU methods.
:::info
This paper is available on arxiv under CC 4.0 license.
:::