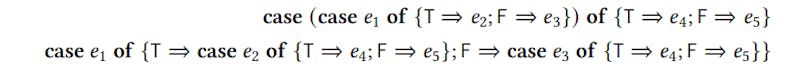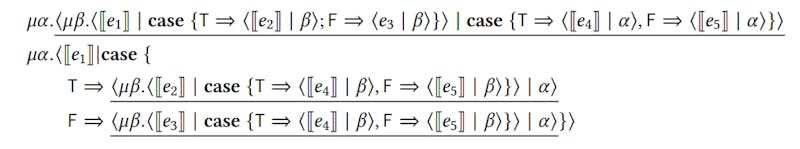Why Compiler Writers Care About Case-of-Case

Table of Links

1. Introduction

2. Translating To Sequent Calculus

   2.1 Arithmetic Expressions

   2.2 Let Bindings

   2.3 Top-level Definitions

   2.4 Algebraic Data and Codata Types

   2.5 First-Class Functions

   2.6 Control Operators

3. Evaluation Within a Context

   3.1 Evaluation Contexts for Fun

   3.2 Focusing on Evaluation in Core

4. Typing Rules

   4.1 Typing Rules for Fun

   4.2 Typing Rules for Core

   4.3 Type Soundness

5. Insights

   5.1 Evaluation Contexts are First Class

   5.2 Data is Dual to Codata

   5.3 Let-Bindings are Dual to Control Operators

   5.4 The Case-of-Case Transformation

   5.5 Direct and Indirect Consumers

   5.6 Call-By-Value, Call-By-Name and Eta-Laws

   5.7 Linear Logic and the Duality of Exceptions

6. Related Work

7. Conclusion, Data Availability Statement, and Acknowledgments

A. The Relationship to the Sequent Calculus

B. Typing Rules for Fun

C. Operational Semantics of label/goto

References

5.3 Let-Bindings are Dual to Control Operators

The label construct in Fun is translated to a 𝜇-binding in Core. Also, when considering the typing rule for label 𝛼 {𝑡 } in Section 4.1, we can see that it directly corresponds to typing a 𝜇-binding with the label 𝛼 being the bound covariable. Similarly, a let-binding is translated to a 𝜇˜-binding and typing a let-binding in Fun closely corresponds to typing a 𝜇˜-term in Core. This way, labels and let-bindings are dual to each other, the same way 𝜇 and 𝜇˜ are. The duality can be extended to other control operators such as call/cc.

As it turns out, the label construct is very closely related to call/cc. There are in fact only two differences. First, label 𝛼 {𝑡 } has the binder 𝛼 for the continuation built into the construct, just as the variation of call/cc named let/cc (which Reynolds [1972] called escape). The second, and more important difference is that the invocation of the continuation captured by label 𝛼 {𝑡 } happens through an explicit language construct goto(𝑡; 𝛼). This makes it easy to give a translation to Core as we can simply insert another 𝜇-binding to discard the remaining continuation at exactly the place where the captured continuation is invoked. In contrast, with call/cc and let/cc the continuation is applied in the same way as a normal function, making it necessary to redefine the variable the captured continuation is bound to when translating to Core. This obscures the duality to let-bindings which is so evident for label and goto.

To see this, here is a translation of let/cc 𝑘 𝑡 to Core

[let/cc 𝑘 𝑡] ≔ 𝜇𝛼.⟨cocase {ap(𝑥, 𝛽) ⇒ ⟨𝑥 | 𝛼⟩} | 𝜇𝑘. ˜ ⟨[𝑡] | 𝛼⟩⟩

The essence of the translation still is that the current continuation is captured by the outer 𝜇 and bound to 𝛼. But now we also have to transform this 𝛼 into a function (the cocase here) which discards its context (here bound to 𝛽) and bind this function to 𝑘, which is done using 𝜇˜. For call/cc, the duality is even more obscured, as there the binder for the continuation is hidden in the function which call/cc is applied to. For the translation, this function must then be applied to the above cocase and the captured continuation 𝛼, resulting in the following term (cf. also [Miquey 2019]).

[call/cc 𝑓] ≔ 𝜇𝛼.⟨[𝑓 ] | ap(cocase {ap(𝑥, 𝛽) ⇒ ⟨𝑥 | 𝛼⟩}, 𝛼)⟩

Other control operators for undelimited continuations can be translated in a similar way. For example, consider Felleisen’s C [Felleisen et al. 1987]. The difference to call/cc is that C discards the current continuation if it is not invoked somewhere in the term C is applied to, whereas call/cc leaves it in place and thus behaves as a no-op if the captured continuation is never invoked. The only change that needs to be made in the translation to Core is that the top-level continuation ⋆ has to be used for the outer cut instead of using the captured continuation. This is most easily seen for a variation of C which has the binder for the continuation built into the operator and where the invocation of the continuation is explicit, similar to label/goto. Calling this variation labelC, we obtain the following translation

[labelC 𝛼 {𝑡 }] ≔ 𝜇𝛼.⟨[𝑡] | ⋆⟩

Here the duality to let-bindings is evident again. The translation for C itself is then obtained in the same way as for call/cc

[C 𝑓 ] ≔ 𝜇𝛼.⟨[𝑓 ] | ap(cocase {ap(𝑥, 𝛽) ⇒ ⟨𝑥 | 𝛼⟩}, ⋆)⟩

5.4 The Case-of-Case Transformation

One important transformation in functional compilers is the case-of-case transformation. Maurer et al. [2017] give the following example of this transformation. The term

n

if (if 𝑒1 then 𝑒2 else 𝑒3) then 𝑒4 else 𝑒5

n

can be replaced by the term

n

if 𝑒1 then (if 𝑒2 then 𝑒4 else 𝑒5) else (if 𝑒3 then 𝑒4 else 𝑒5).

n

Logicians call these kinds of transformations commutative conversions, and they play an important role in the study of the sequent calculus. But as Maurer et al. [2017] show, they are also important for compiler writers who want to generate efficient code.

n

In the 𝜆𝜇𝜇˜-calculus, commuting conversions don’t have to be implemented as a special compiler pass. They fall out for free as a special instance of 𝜇-reductions! Let us illustrate this point by translating Maurer et al.’s example into the 𝜆𝜇𝜇˜-calculus. First, let us translate the two examples using pattern-matching syntax:

n

Let us now translate these two terms into the 𝜆𝜇𝜇˜-calculus:

n

n

We can see that just by reducing all of the underlined redexes we reduce both of these examples to the same term.

:::info
Authors:

(1) David Binder, University of Tübingen, Germany;

(2) Marco Tzschentke, University of Tübingen, Germany;

(3) Marius Muller, University of Tübingen, Germany;

(4) Klaus Ostermann, University of Tübingen, Germany.

:::

---

:::info
This paper is available on arxiv under CC BY 4.0 license.

:::