Bernstein’s Concentration Inequality In Equivalence Testing

:::info
Authors:

(1) Diptarka Chakraborty, National University of Singapore, Singapore

(2) Sourav Chakraborty, Indian Statistical Institute, Kolkata;

(3) Gunjan Kumar, National University of Singapore, Singapore;

(4) Kuldeep S. Meel, University of Toronto, Toronto.

:::

Table of Links

Abstract and 1 Introduction

2 Notations and Preliminaries

3 Related Work

4 An Efficient One-Round Adaptive Algorithm and 4.1 High-Level Overview

4.2 Algorithm Description

4.3 Technical Analysis

5 Conclusion

6 Acknowledgements and References

A Missing Proofs

B An O(log log n)-query fully adaptive algorithm

A MISSING PROOFS

Therefore, by additive Chernoff bound (Lemma 2.3), the value et = EstTail(D, i, S, β, b, m) returned by the algorithm satisfies

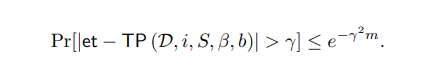
To prove Claims 4.10, 4.11 and 4.12, we will use the following concentration inequality that directly follows from Bernstein’s concentration inequality.

:::info
This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.

:::